The Best Shape Dining Table for Parties and Large Families (Calculations and Proof!)

Table of contents

I’ll just say this: If you’re looking for a big table, look no further.

We’re here to help! We’ll tell you which dining table shape is best for parties and large families.

What is the best-shaped dining table for a large group?

A rectangular dining table is generally considered the best shape for a large group.

Rectangular dining tables provide the most surface area and can accommodate the most people. They also allow for easy placement of chairs and can be positioned against a wall, saving space in a room.

Also, rectangular tables are versatile and can be used for many things, like hosting a dinner party, working from home, or playing games with friends and family. Therefore, if you have a large group of people to seat, a rectangular dining table would be the best choice.

By determining a few criteria such as perimeter and taking into consideration the size and surface area of a tabletop, you’ll likely find that the table shape that fits the most people is a rectangle. This conclusion is based on comparing a standard-sized surface area across all shapes and then comparing their outer edge parameter to this standard surface area number. This results in a ratio of space around the table to the size of the table, which we use to compare different-shaped tables.

Why exactly are rectangular tables the best for large groups?

The long, straight edges of a rectangular table allow for the placement of chairs on either side, making it easy to seat many people.

When it comes to the size of the table, a rectangular table should be at least 36 inches (91 cm) wide to allow for comfortable place settings, with additional space for dishes, glasses, and table settings.

The length of the table will depend on the number of people it needs to accommodate. As a general rule of thumb, each person should have at least 24 inches (61 cm) of space along the table, although some people may require more space if they are larger or if they need to use a wheelchair.

For example, if you are hosting a large dinner party for 12 people, a rectangular table that is 8 feet (244 cm) long and 3 feet (91 cm) wide would be a good size. This would allow for each person to have 2 feet (61 cm) of space along the table, with additional space for dishes and table settings.

It’s also important to consider the available space in the room when choosing a rectangular table for a large group. A rectangular table can be a good choice if the room is long and narrow, as it can be placed lengthwise along the wall.

However, if the room is square or small, a rectangular table may not be the best choice, as it can take up a lot of space and make it difficult to move around the room.

What kind of shapes do dining tables come in?

Dining tables can come in a variety of different shapes. The tabletops are important because it’s the size and shape of the tabletop that determines how many people can fit on it.

Some of the most common tabletops you’ll find in any household are square, rectangle, circle, and oval.

In this article, I’m going to ignore the less common ones that have odd shapes and such so you won’t get answers about the star and trapezoid-shaped tabletops here.

What makes rectangles the best at holding the most people?

The answer has to do with math. When determining how many people can surround a table, we must look at the perimeter of a table.

The bigger the perimeter, the more people it can potentially fit around it.

In order to determine the perimeter of a rectangle, we simply have to multiply the width by 2 and add it to the height times 2.

Let’s say for example that the table we want to find the perimeter of is 6ft (72in) by 4ft (48in). When you calculate the two numbers, we get 20ft (240in) all around.

What this means is that if you stretched a ruler all the way around the outside edges of the table, you’d need 20ft (240in) of the ruler to completely wrap around the entire edge of the tabletop.

Now if each person required 24 inches worth of space including elbow room, we would likely be able to fit 240 inches divided by 24in which equals 10 people on that one table.

But why does a rectangular table beat out a square, circle, and oval?

The proof behind a rectangle’s shape and capacity

Let’s say you have a rectangular table that is 4ft by 6ft in tabletop size. In order to get the area of a rectangle, it’s Area = Length x Width.

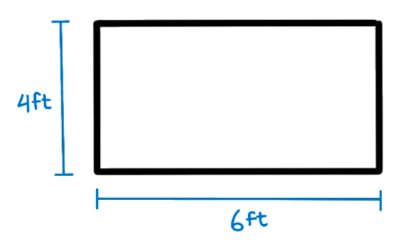
That means 4 x 6 = 24ft².

Now, I’ve come up with a ratio that will tell us how efficient the size of a table is compared to the space it has on its perimeter. Simply divide the area of the table by the length of the outer edge with is the perimeter.

The formula for perimeter = 2 x Length + 2 x Width.

This gives us a total of 20ft worth of space around this rectangular table.

If you find the ratio of 20ft to 24ft², then you get approximately an 83.33% edge to area ratio.

Why a square-shaped table can’t hold as many people as a rectangular table

One thing I’m not taking into account is the space required for the table. The ratio and method I will use assumes that all tables have roughly the same surface area which is 24ft².

In any other scenario, if you have a small home or very little dining space, then it might be important to see what would fit. However, with a 24ft² table, my calculations will make it fair for all the sizes we are going to discuss.

A square table that has an area of 24ft² is what we will compare next.

A square has 4 equal corners and so if we have the surface area, and we want to get the length of just one side of the square, we simply need to find the square root of the area.

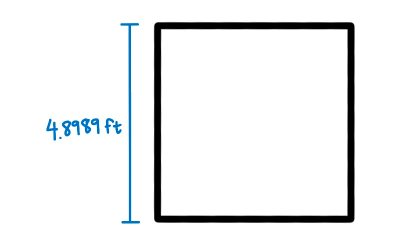
Taking the square root of 24ft² gives us approximately 4.8989ft which is the length of 1 of the 4 equal sides of the square.

We now need to find the length of the edges around all 4 corners of the table, so we simply just multiply 4.8989ft x 4 and we get 19.5956ft.

Applying the ratio of length to the area (19.5956/24), we get 81.6483%.

When comparing this ratio to a rectangle with the same standard surface area of 24ft², you can see that you get slightly less room on a table.

Why a circle-shaped table can’t hold as many people as a rectangular table

This is going to be a bit different in the formula.

We already know that we are going to use our own standard 24ft² as the surface area of the circle. But now we need to find the perimeter of the circle which is also known as the circumference of the circle.

The formula to find that is circumference = 2 x Pi x radius.

In order to find the radius, we’re going to have to work backward from the surface area formula of a circle which is Area = Pi x r².

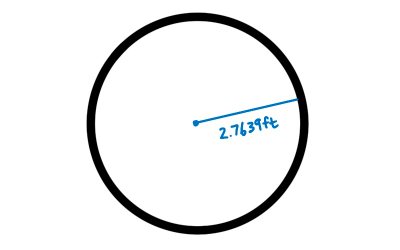
This isn’t a math course, just a proof of concept and so what I found was that a perfect circle with a surface area of 24ft² has a radius of 2.7639ft.

Now we can use the radius to plug back into our circumference formula (remember, that’s why we were looking for the radius in the first place) and we get a circumference of 17.3661ft.

Plugging in the numbers we know back into the length to area ratio we get (17.3661/24) = 72.45%.

That’s much smaller than a rectangle.

What an oval-shaped table can’t hold as many people as a rectangular table

Now I don’t think I can go over the math of an oval table because of the complexity. My math didn’t go very far in school But if you just think about it..

An oval is somewhat a combination of a rectangle or circle, and my best guess at what you end up getting is a ratio in between the results for a rectangle and a circle.

What should you consider when choosing a shape for your dining table?

When choosing a shape for your dining table, two key factors to consider are the number of people that can sit on it and the size of the table.

Amount of people

The number of people that can sit at a dining table will depend on its shape and size.

Rectangular tables tend to seat the most people, as they have a long, straight edge that allows for the placement of chairs on either side.

Square tables usually have less room for people to sit, while round tables can seat the same number of people as square tables but in a more flexible way.

Size of the table

The size of the dining table will depend on the available space in the room and the number of people you want to seat.

A general rule of thumb is to leave at least 36 inches (91 cm) between the edge of the table and any walls or other furniture in the room to allow for comfortable seating and movement around the table.

The size of the table should also be proportionate to the size of the room.

The best shapes for dining tables for large groups

Rectangular tables

Rectangular tables allow for easy placement against a wall, saving space in a room. However, the size and shape of the room should be taken into consideration, as a large rectangular table may not fit well in a small dining room.

Square tables

Square tables can also be a good choice for large families, but they typically seat fewer people than rectangular tables. Square tables are best suited for smaller groups of 4-64–6 people. However, if the square table is large enough, it can accommodate more people.

Round tables

Round tables can be a good choice for large families if they are large enough to accommodate everyone comfortably. The lack of corners on a round table can make it easier to navigate around the table and can create a more intimate atmosphere. However, round tables typically seat fewer people than rectangular or square tables of the same size.

Oval tables

Oval tables are similar to rectangular tables in terms of seating capacity, but their rounded ends can make them more space-efficient. The oval shape also creates a more fluid and organic flow in the room. However, like rectangular tables, the size and shape of the room should be taken into consideration when choosing an oval table.

Conclusion

Now I know these ratios seem pretty small and I understand. This article simply sets out on a mission to prove a fact.

I wouldn’t use this information directly to make a decision on the shape of a table that I plan to buy. The results are just too small to make any impact.

Just trust yourself on the kind of dining table you personally would prefer. Forget about the shape.

As a result of my findings, the difference between a rectangle and a circle is merely a few inches. Now unless you have a massive table, and you have several people who are trying to cramp into that one table, then maybe this might be something you might want to consider more.

I can only think about restaurants and bars that might be at least somewhat interested in this. However, when it comes down to it, it’s all about preference.

Other interesting articles: